The actual assumptions underlying certain "reductionism" or "holism"

I have sometimes gotten annoyed at people arguing over whether "the whole is greater than the sum of it's parts."

I think there genuinely is a difference between thinking in a "reductionist mindset" and a "hollist mindset", but I haven't seen either one actually get a good description.

First, I hate the phrase "the whole is greater than the sum of its parts" because it works on a linguistic trick.

What does "sum" mean? Or better yet, what operation are you calling a "sum"? If the operation that you are calling a "sum" doesn't reproduce the whole, why did you call it "sum" in the first place?

For the good of humanity, here is a list of specific properties that a system may or may not have, which I think people are often implicitly trying to gesture to.

Approximation-ism

Sure we don't know quantities exactly, and we can't solve for an exact solution, but we can get arbitrarily close approximations, or if not arbitrarily close, close enough for all of our actual use cases. Example:

• Ignore air resistance
• Many NP-hard problems can't be exactly solved in poly time, but you can get good approximations in poly time

Arch Nemesis: Chaotic Systems Chaos is "When the present determines the future, but the approximate present does not approximately determine the future." Double pendulums are chaotic. This gif starts three pendulums in almost the same state. They start correlated, but quickly become independent. The point, your epsilon of measurement error might actually matter a ton.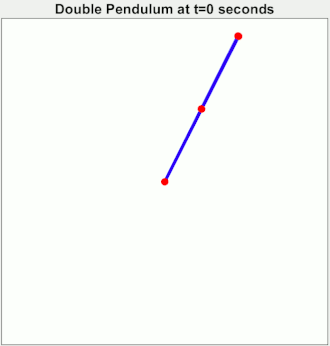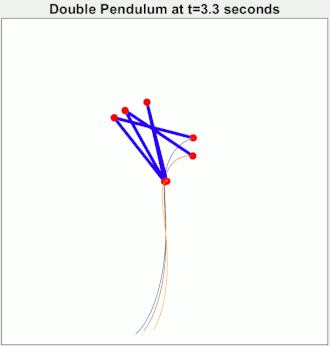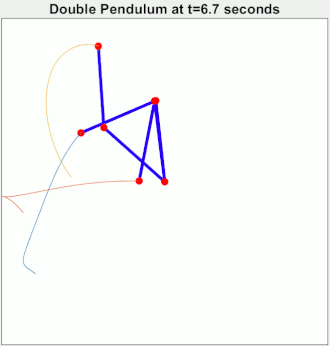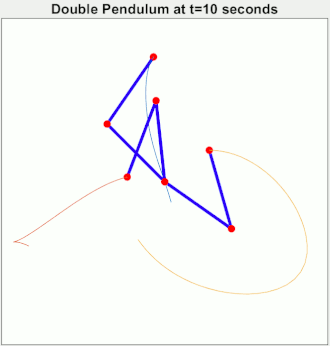

Locality

The only things that matter for predicting or explaining what is happening at X is what is near X. As things get farther from X, their effects rapidly become negligible. Examples:

• Gravity falls off with 1/r^2.

Arch Nemesis: Spooky Action at a Distance

The stuff that may matter may be nowhere near where X is.

• People's moods (cuz internet)
• Quantum entaglement (no idea what's actually up with this)
• Using global variables in code
• Shared memory between processes in code

Monotonicity

As you add more terms / get more information / make more observations, you are strictly getting closer to the correct answer. Each new prediction is a strict subset of previous ones. I might also mix this in with "80/20ism" or "marginal returns-ism". The first several terms do most of the work. Examples:

• Taylor series approximations are monotonic, you strictly approach a perfect fit, and it's clear "where things are heading"
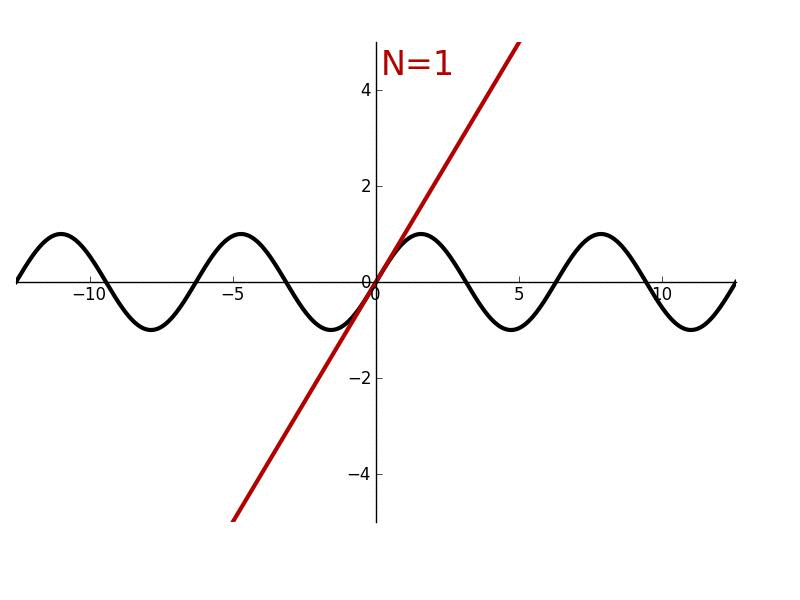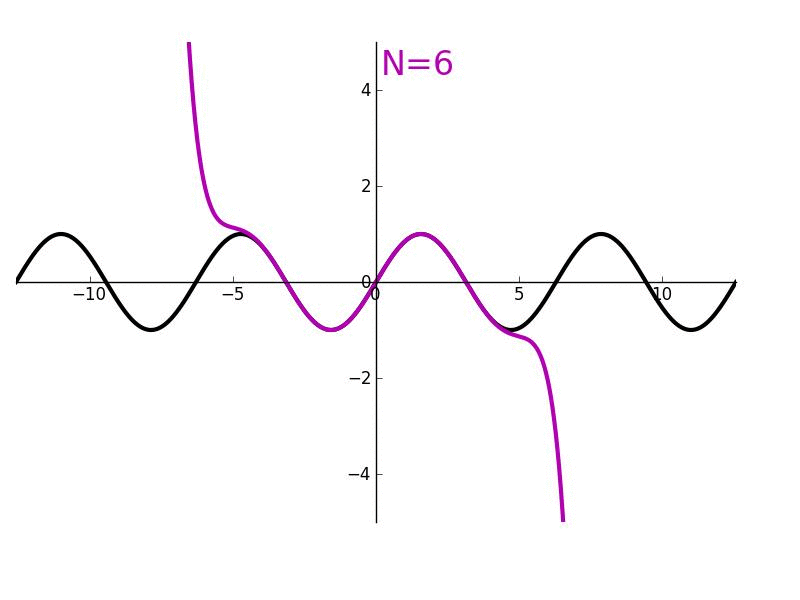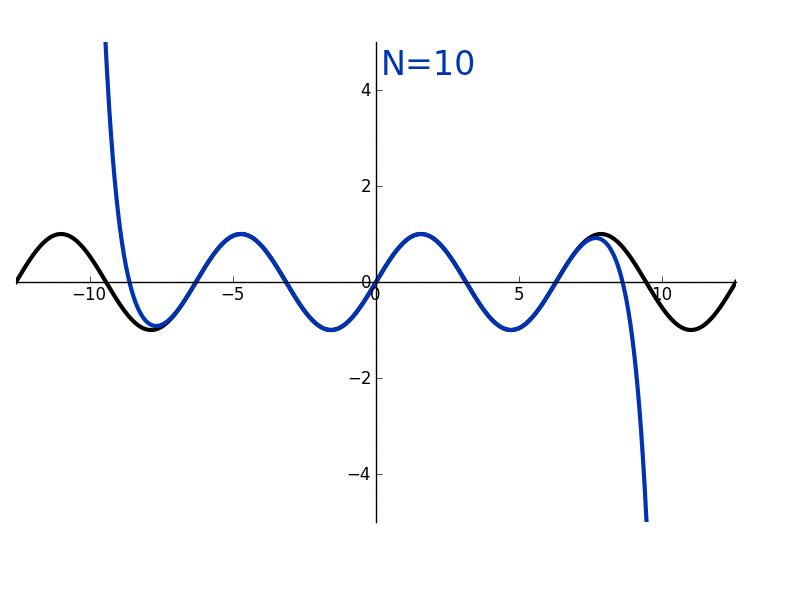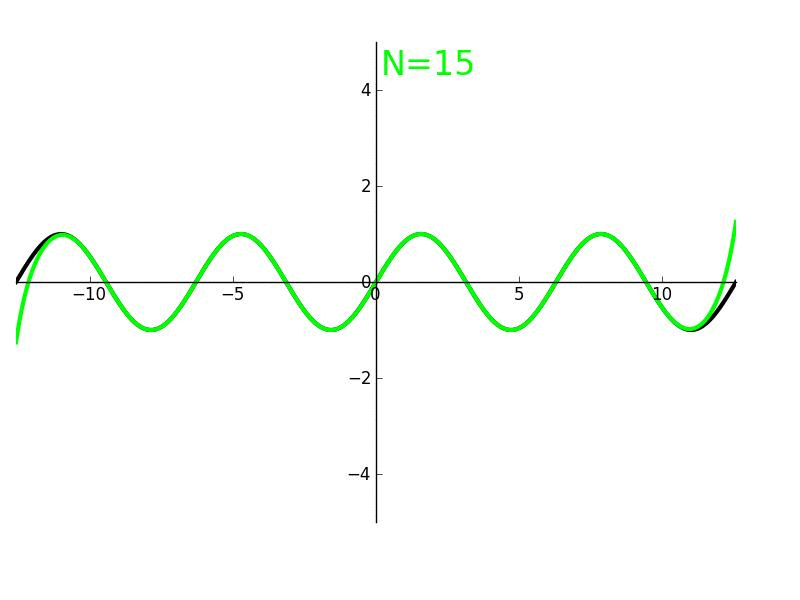
• 20 questions
• Binary search
• Statistic, keep sampling the population, approach the "true" value
• At the point where your approximation is centered, taylor series also exemplify marginal-returns, the first few terms get you the bulk of the accuracy, and the rest are small precision boosts.
• Math, you only build, you never loose info (for the most part).
• Top level chess, not that many "upsets", it becomes a game of

Arch Nemesis: "It's not over till the fat lady sings" As you get more info, what the answer looks like could radically change. An "upset victory" can always happen at the 11th hour.

• Kuhn like paradigm shifts (the paradigm is non-monotonic, not your "total explanatory power")

Modularity

As long as you meet the requirements of the minimal interface, all parts are the same and can be swapped out for each other. The whole system is made of modules that interlock nicely at clear interfaces allowing separation of concerns. Examples:

• Literal interfaces in code
• Dependency injection (for swapping in mocks and fakes for testing code)
• I can change the tires on my car.
• Strict contract bound business partnership

Arch Nemesis: Organic intermingled boundaries There aren't clean edges between parts. Things are deeply interconnected. Parts can me worked on in isolation.

• When code starts to depend on implementation details not specified in the API and you can't change anything without breaking people's shit.
• Body rejecting prosthetic organs (sometimes) even thought they "fulfill the role".
• Romantic relationship with cohabitation

Composability

When composing systems with operation Y, property X is preserved (fav post on composition). Examples:

• Proof tree (as long as the child nodes of your top level statements have valid proof, you're fine)

Arch Nemesis: Emergence

• Just because all of your dependencies have X security guarantee, doesn't mean that using these dependencies together will still guarantee X.
• The property "getting along well together" is not preserved when composing groups of friend with the "smoosh them into one big group" operation.
• Understanding the words of a sentence doesn't have to imply that I understand the whole sentence.

Honorable mentions

• Memorylessness vs Memoryfullness
• A whole host of "nice" properties
  • Transitivity
  • Communativity
  • Associativity

A thing that's really interesting about several of these is the way that they are the dual or their arch nemesis. You can make any system where memory is relevant "memoryless" by encoding all of the history into the current state. As such, a critique should never be "You aren't taking history into account!" but instead "you think you need thiiiiiis much historical state to predict the future, but really you need thiiis much". Likewise for modularity, if you make your interface include all the information about a part, then boom, thinks are always modular... except you lost the actual utility of having a small easy to reason about interface.

I think software engineering is a great domain to study this. Basically every desirable property you could have of a system you want to science exists a design principle for "making understandable code that we can reuse". You can find code bases that do a good some of enforcing locality, and others that fail miserably. You can see the practical side of all this. "Oh, this is how much locality is necessary for me to easily solve the problem."

For any given system in any given domain, there is a factual question of "does locality apply?" "can we reason monotonically about it?" or "is this chaotic?". I hope to not have to have conversations where we accuse each other of being "too reductionistic" or "too holistic" and instead can use some of the language here to say "you're assuming locality, which doesn't hold cuz ABC" or "you're failing because you aren't taking advantage of modularity, so try XYZ".